Merge sort is a sorting technique based on divide and conquer technique. With worst-case time complexity being Ο(n log n), it is one of the most respected algorithms.

Merge sort first divides the array into equal halves and then combines them in a sorted manner.

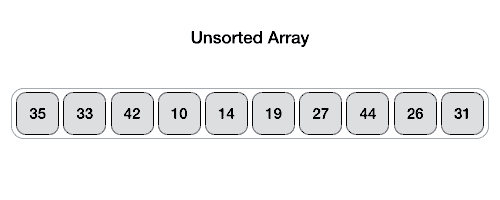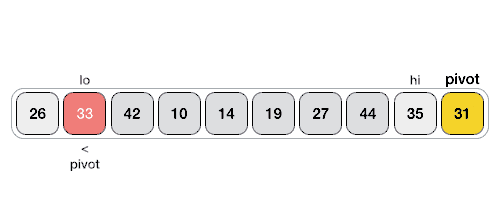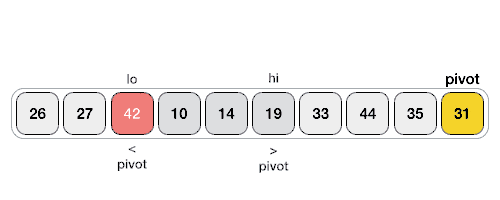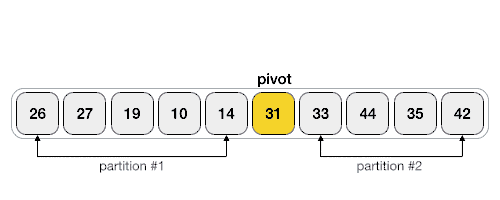
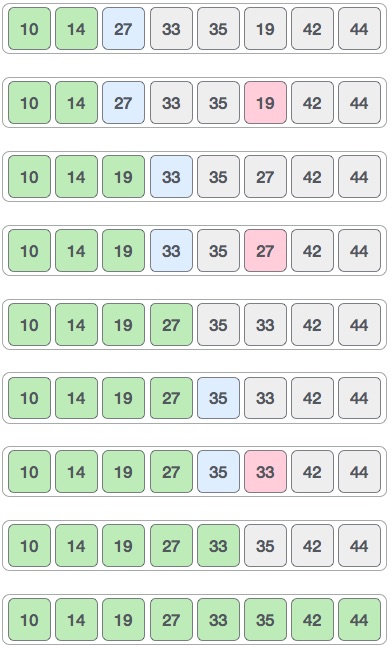
To understand merge sort, we take an unsorted array as the following −

We know that merge sort first divides the whole array iteratively into equal halves unless the atomic values are achieved. We see here that an array of 8 items is divided into two arrays of size 4.

This does not change the sequence of appearance of items in the original. Now we divide these two arrays into halves.

We further divide these arrays and we achieve atomic value which can no more be divided.

Now, we combine them in exactly the same manner as they were broken down. Please note the color codes given to these lists.

We first compare the element for each list and then combine them into another list in a sorted manner. We see that 14 and 33 are in sorted positions. We compare 27 and 10 and in the target list of 2 values we put 10 first, followed by 27. We change the order of 19 and 35 whereas 42 and 44 are placed sequentially.

In the next iteration of the combining phase, we compare lists of two data values, and merge them into a list of found data values placing all in a sorted order.

After the final merging, the list should look like this −

Now we should learn some programming aspects of merge sorting.

C code:

#include <stdio.h>

#include <stdlib.h>

void merg(int *a,int n)

{

int i,j,l,r;

for(i=0;i<n;i++)

printf("%d",a[i]);

printf("\n");

if(n<2)

return;

l=n/2;

r=n-l;

int *le=malloc(sizeof(int)*l);

int *ri=malloc(sizeof(int)*r);

for(i=0;i<l;i++)

le[i]=a[i];

for(i=l;i<n;i++)

ri[i-l]=a[i];

merg(le,l);

merg(ri,r);

mergee(le,l,ri,r,a,n);

}

void mergee(int *a,int l,int *b,int r,int *c,int n)

{

int i,j,k;

i=j=k=0;

while(i<l&&j<r)

{

if(a[i]<=b[j])

c[k++]=a[i++];

else

c[k++]=b[j++];

}

while(i<l)

c[k++]=a[i++];

while(j<r)

c[k++]=b[j++];

}

int dmain(int argc, char *argv[]) {

int *p,i,n;

scanf("%d",&n);

p=malloc(sizeof(int)*n);

for(i=0;i<n;i++)

scanf("%d",p+i);

merg(p,n);

for(i=0;i<n;i++)

printf("%d",*(p+i));

return 0;

}

Quick sort is a highly efficient sorting algorithm and is based on partitioning of array of data into smaller arrays. A large array is partitioned into two arrays one of which holds values smaller than the specified value, say pivot, based on which the partition is made and another array holds values greater than the pivot value.

Quick sort partitions an array and then calls itself recursively twice to sort the two resulting subarrays. This algorithm is quite efficient for large-sized data sets as its average and worst case complexity are of Ο(n²), where n is the number of items.

Following animated representation explains how to find the pivot value in an array.

The pivot value divides the list into two parts. And recursively, we find the pivot for each sub-lists until all lists contains only one element.

C code:

#include <stdio.h>

#include <stdlib.h>

void quick(int *a,int s,int e)

{

if(s<e)

{

int p;

p=partion(a,s,e);

quick(a,s,p-1);

quick(a,p+1,e);

}

}

int partion(int *a,int s,int e)

{

int i,j,pi,p;

p=a[e];

pi=s;

for(i=s;i<e;i++)

{

if(a[i]<=p)

{

j=a[i];

a[i]=a[pi];

a[pi]=j;

pi++;

}

}

j=a[e];

a[e]=a[pi];

a[pi]=j;

return pi;

}

int main(int argc, char *argv[]) {

int *p,i,n;

scanf("%d",&n);

p=malloc(sizeof(int)*n);

for(i=0;i<n;i++)

scanf("%d",p+i);

quick(p,0,n-1);

for(i=0;i<n;i++)

printf("%d",*(p+i));

return 0;

}

Selection sort is a simple sorting algorithm. This sorting algorithm is an in-place comparison-based algorithm in which the list is divided into two parts, the sorted part at the left end and the unsorted part at the right end. Initially, the sorted part is empty and the unsorted part is the entire list.

The smallest element is selected from the unsorted array and swapped with the leftmost element, and that element becomes a part of the sorted array. This process continues moving unsorted array boundary by one element to the right.

This algorithm is not suitable for large data sets as its average and worst case complexities are of Ο(n²), where n is the number of items.

Consider the following depicted array as an example.

For the first position in the sorted list, the whole list is scanned sequentially. The first position where 14 is stored presently, we search the whole list and find that 10 is the lowest value.

So we replace 14 with 10. After one iteration 10, which happens to be the minimum value in the list, appears in the first position of the sorted list.

For the second position, where 33 is residing, we start scanning the rest of the list in a linear manner.

We find that 14 is the second lowest value in the list and it should appear at the second place. We swap these values.

After two iterations, two least values are positioned at the beginning in a sorted manner.

The same process is applied to the rest of the items in the array.

Following is a pictorial depiction of the entire sorting process −

Now, let us learn some programming aspects of selection sort.

C code:

#include <stdio.h>

#include <stdlib.h>

void selec(int *p,int n)

{

int i,j,min,t;

for(i=0;i<n-1;i++)

{min=i;

for(j=i+1;j<n;j++)

if(p[min]>p[j])

min=j;

t=p[min];

p[min]=p[i];

p[i]=t;

}

}

int amain(int argc, char *argv[]) {

int *p,i,n;

scanf("%d",&n);

p=malloc(sizeof(int)*n);

for(i=0;i<n;i++)

scanf("%d",p+i);

selec(p,n);

for(i=0;i<n;i++)

printf("%d",*(p+i));

return 0;

}

We take an unsorted array for our example.

Insertion sort compares the first two elements.

It finds that both 14 and 33 are already in ascending order. For now, 14 is in sorted sub-list.

Insertion sort moves ahead and compares 33 with 27.

And finds that 33 is not in the correct position.

It swaps 33 with 27. It also checks with all the elements of sorted sub-list. Here we see that the sorted sub-list has only one element 14, and 27 is greater than 14. Hence, the sorted sub-list remains sorted after swapping.

By now we have 14 and 27 in the sorted sub-list. Next, it compares 33 with 10.

These values are not in a sorted order.

So we swap them.

However, swapping makes 27 and 10 unsorted.

Hence, we swap them too.

Again we find 14 and 10 in an unsorted order.

We swap them again. By the end of third iteration, we have a sorted sub-list of 4 items.

This process goes on until all the unsorted values are covered in a sorted sub-list.

C Code:

#include <stdio.h>

#include <stdlib.h>

void ins(int *a,int n)

{

int i,j,val,t;

for(i=1;i<n;i++)

{val=a[i];

t=i;

while(t>0&&a[t-1]>val)

{

a[t]=a[t-1];

t--;

}

a[t]=val;

}

}

int bmain(int argc, char *argv[]) {

int *p,i,n;

scanf("%d",&n);

p=malloc(sizeof(int)*n);

for(i=0;i<n;i++)

scanf("%d",p+i);

ins(p,n);

for(i=0;i<n;i++)

printf("%d",*(p+i));

return 0;

}